Coloring In Graph Theory - Coloring Pages For Kids
Harmonious Coloring Wikipedia
Graph Coloring Greedy Algorithm O V 2 E Time Complexity
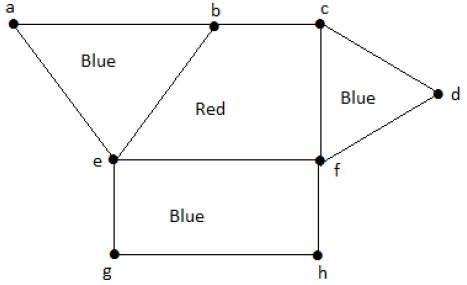
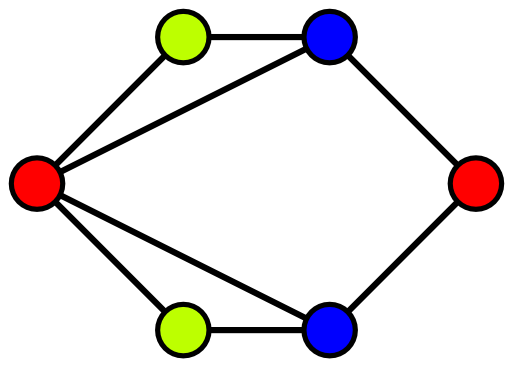
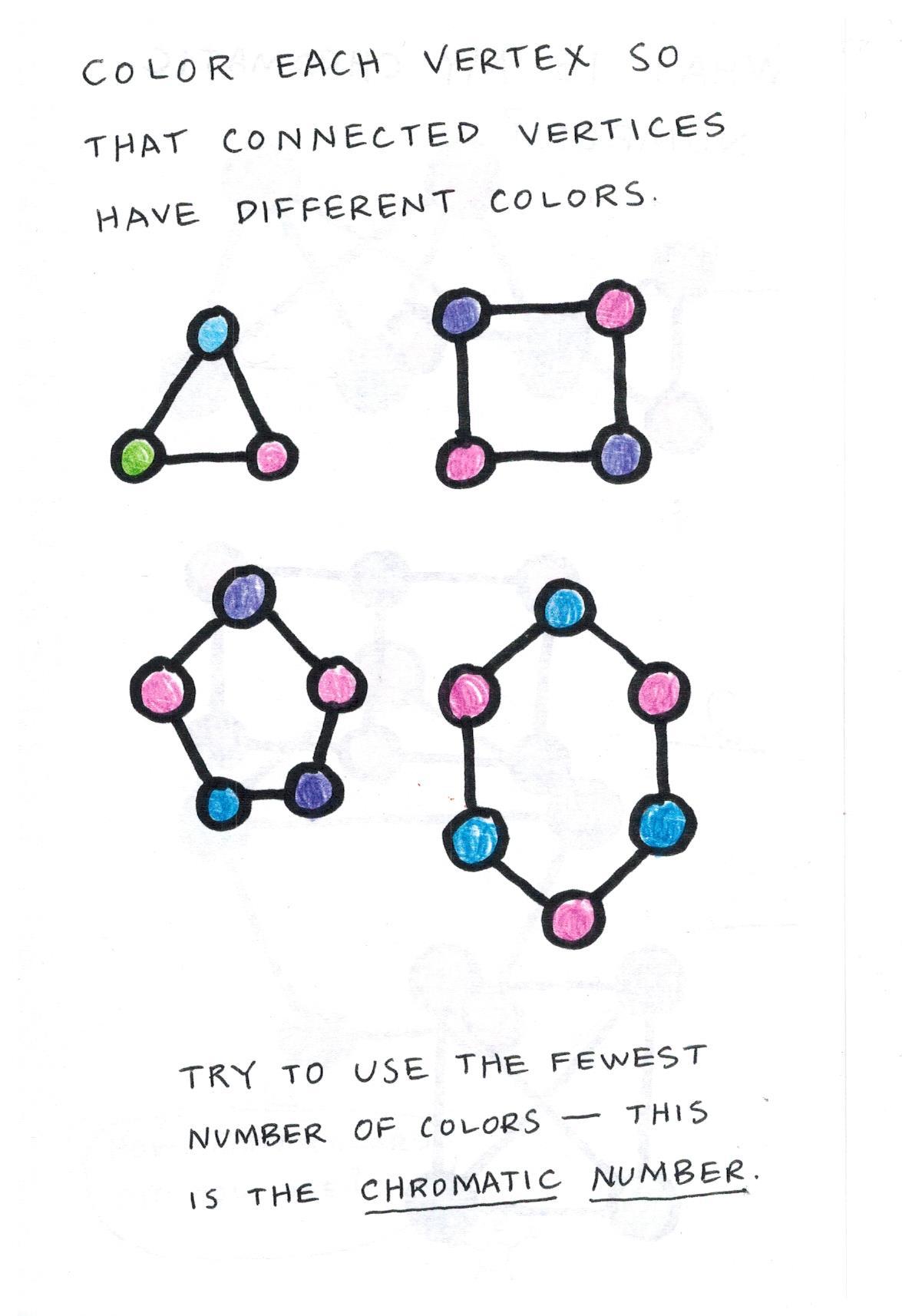
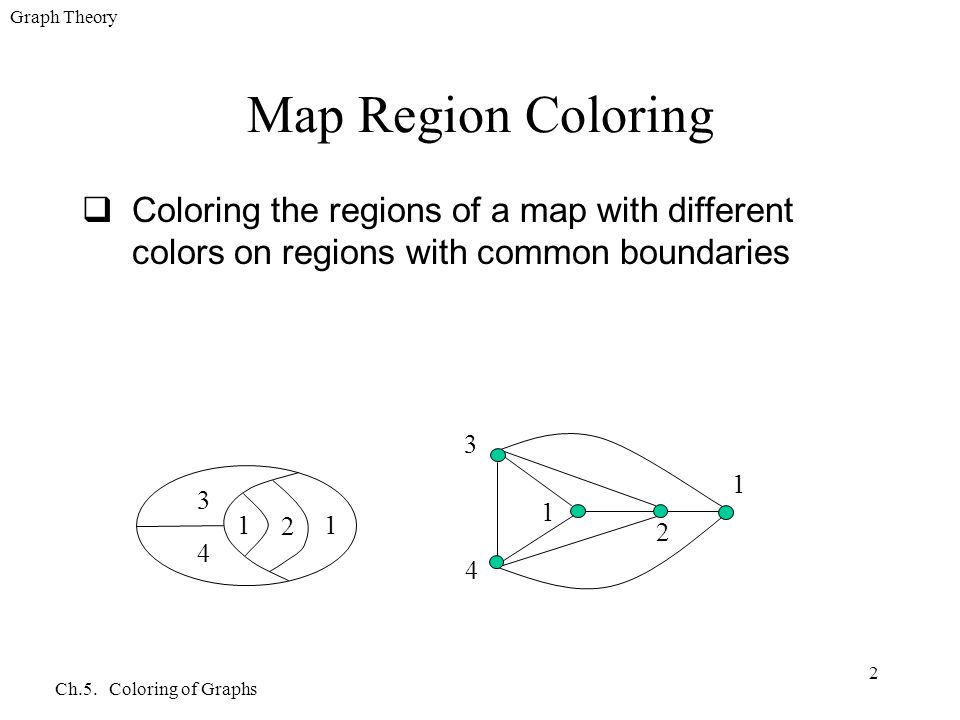
First let us define the constraint of coloring in a formal way coloring a coloring of a simple graph is the assignment of a color to each vertex of the graph such that no two adjacent vertices are assigned the same color.
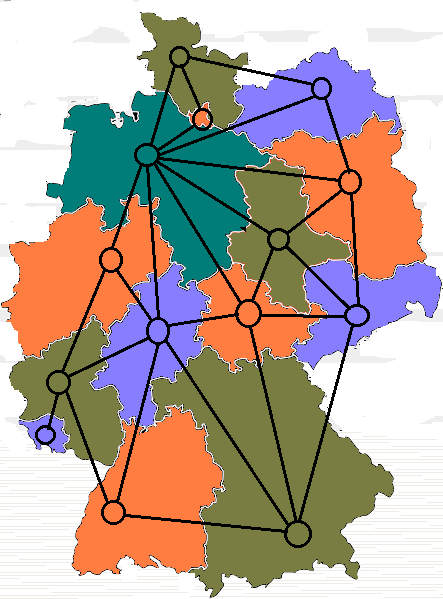
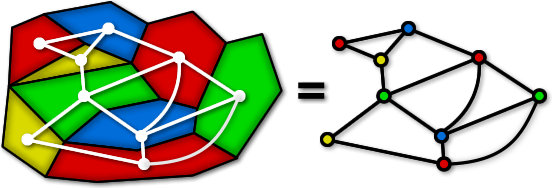
Coloring in graph theory. Hence each vertex requires a new color. In a graph no two adjacent vertices adjacent edges or adjacent regions are colored with minimum number of colors. Graph theory coloring. A vertex coloring is an assignment of labels or colors to each vertex of a graph such that no edge connects two identically colored vertices.
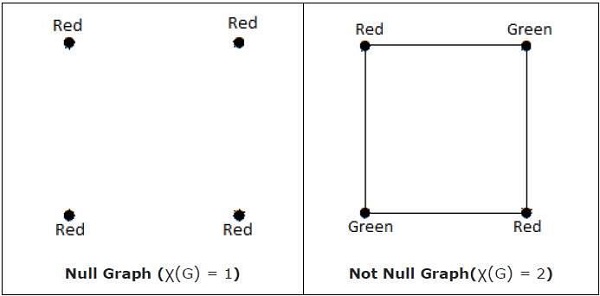
This question along with other similar ones have generated a lot of results in graph theory. Coloring problems in graph theory kevin moss iowa state university follow this and additional works athttpslibdriastateeduetd part of thecomputer sciences commons and themathematics commons this dissertation is brought to you for free and open access by the iowa state university capstones theses and dissertations at iowa state university. 1007 3137 3157 3203 4115 3261 4156 4118. Chromatic number of a graph is the minimum number of colors required to properly color the graph.
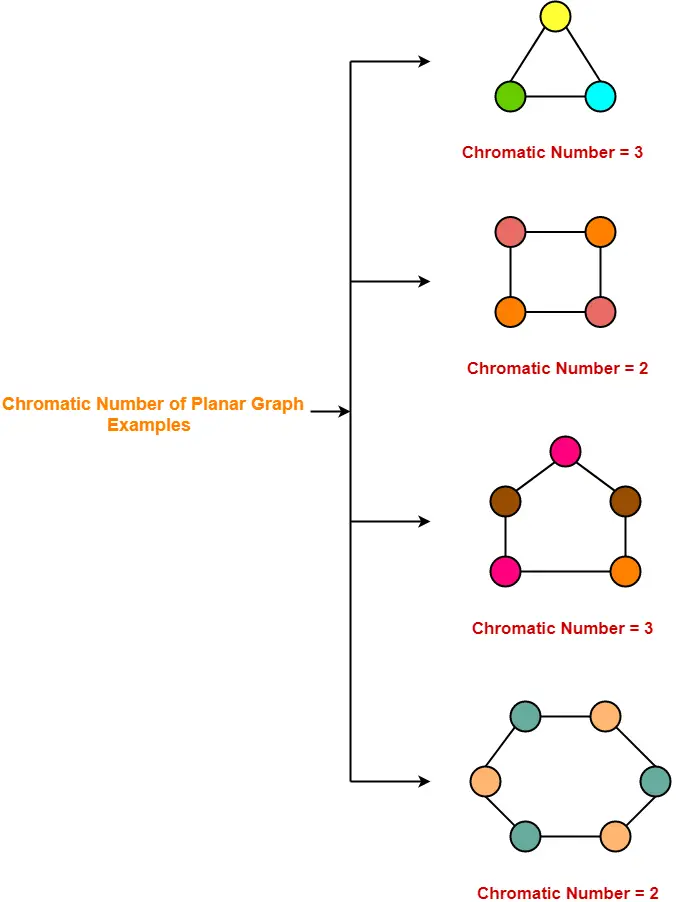
Graph coloring problem is to assign colors to certain elements of a graph subject to certain constraints. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color. A graph coloring is an assignment of labels called colors to the vertices of a graph such that no two adjacent vertices share the same color. Such a coloring is known as a minimum vertex coloring and the minimum number of colors which with the vertices of a graph g may be colored is called the.
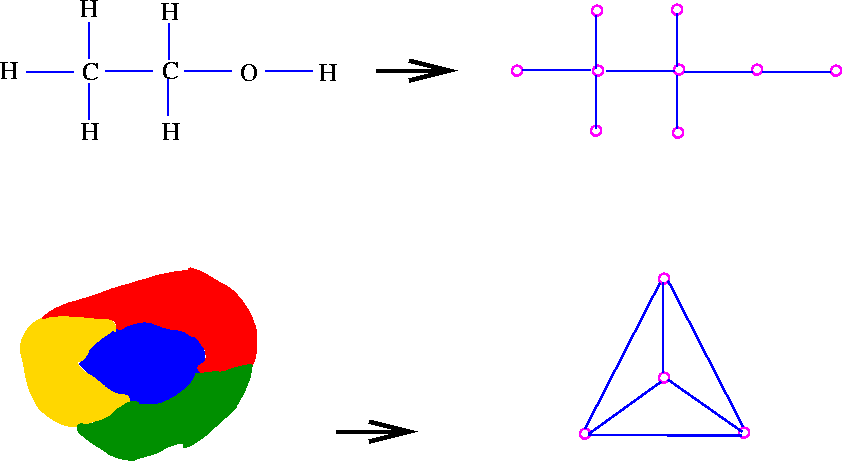
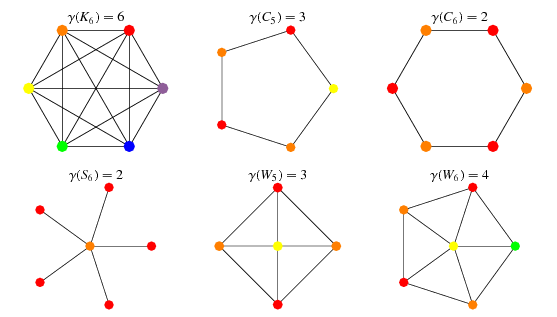
In the complete graph each vertex is adjacent to remaining n1 vertices. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. The chromatic number x g chig x g of a graph g g g is the minimal number of colors for which such an. Graph coloring is nothing but a simple way of labelling graph components such as vertices edges and regions under some constraints.
It is impossible to color the graph with 2 colors so the graph has chromatic number 3. A graph coloring for a graph with 6 vertices. Hence the chromatic number of kn n. Vertex coloring is the most common graph coloring problem.
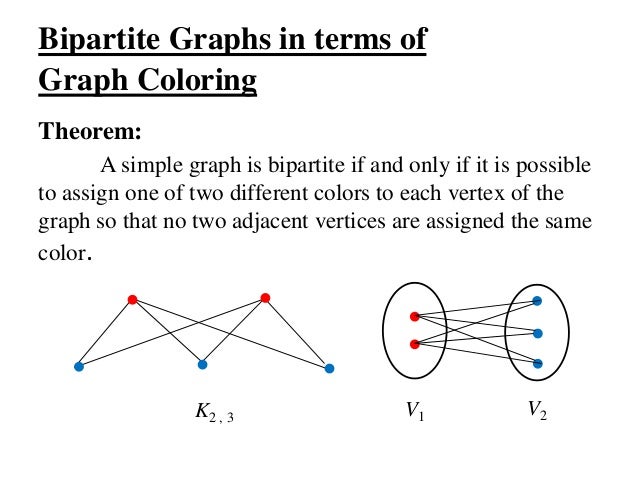
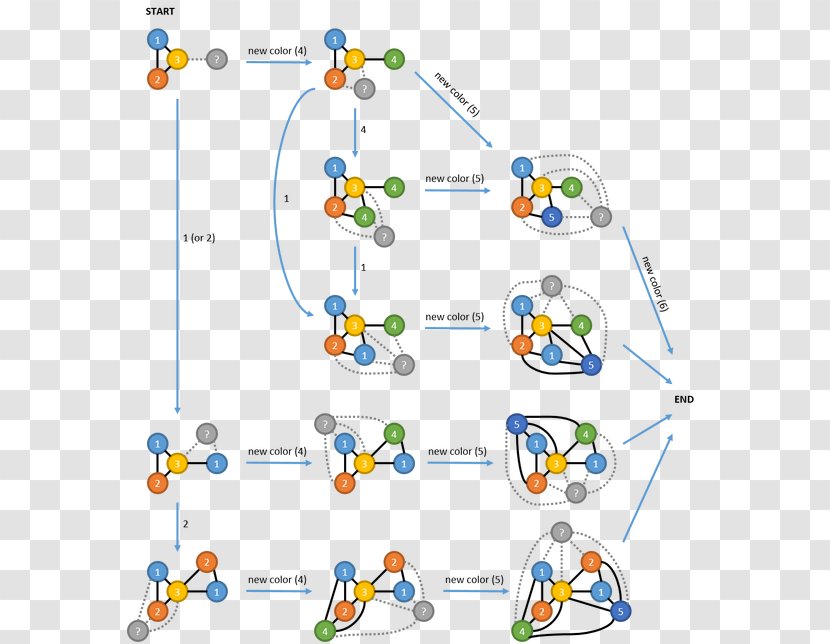
In graph theory graph coloring is a special case of graph labeling. Two vertices are connected with an edge if the corresponding courses have a student in common. Applications of graph coloring graph coloring is one of the most important concepts in graph theory. The problem is given m colors find a way of coloring the vertices of a graph such that no two adjacent vertices are colored using same color.
Graph coloring and scheduling convert problem into a graph coloring problem. Courses are represented by vertices. Graph coloring in graph theory graph coloring is a process of assigning colors to the vertices such that no two adjacent vertices get the same color.
Fractional Graph Theory A Rational Approach To The Theory Of Graphs Fractional Coloring Pattern Mathematical Theory Branch Symmetry Name Png Pngwing
Graph Theory Coloring Tutorialspoint
Graph Colouring Lecture 20 Nov 25 This Lecture Graph Coloring Is Another Important Problem In Graph Theory It Also Has Many Applications Including Ppt Download
Brooks Theorem Line Graph Graph Coloring Graph Theory Vertex Regular Graph Biconnected Component Biconnected Graph Png Nextpng
Vertex Coloring Martin Thoma
Graph Coloring Mathematics Graph Theory Eulerian Path Png Clipart Addition Algebra Angle Body Jewelry Circle Free
20 Mind Blowing Reasons Why Star Coloring In Graph Theory With Images Coloring Pages Storm King Art Center Line Artwork
Graph Theory
Graph Theory
Graph Coloring And Chromatic Numbers Brilliant Math Science Wiki
Map Coloring And Conflict Resolution Occupy Math
Hadwiger Conjecture Graph Theory Coloring Mathematics Disjoint Transparent Png
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcq7v6tv Ambexwpnv1bh1wsm5ze57lfhi Sa3rbp6p W Dgcw6j Usqp Cau
Graph Coloring Wikipedia
Graph Coloring Set 2 Greedy Algorithm Geeksforgeeks
Graph Theory
Graph Coloring Graph Theory Planar Graph Four Color Theorem Mathematics Text Color Png Pngegg
Vertex Coloring Of A Graph With Webmathematica Download Scientific Diagram
Graph Theory Graph Coloring Petersen Graph Chvatal Graph Png 1200x1200px Graph Theory Area Blue Diagram Donald
Exact Coloring Wikipedia
Mathematician Disproves Hedetniemi S Graph Theory Conjecture Quanta Magazine
Graph Theory Edge Coloring Gate Overflow
Fractional Coloring From Wolfram Mathworld
Graph Theory Ch 5 Coloring Of Graphs 1 Chapter 5 Coloring Of Graphs Ppt Download
Edge Coloring Of Bipartite Graphs Mathematics Stack Exchange
Application Of Graph Coloring In Map Coloring And Gsm Mobile Phone Networks Graph Theory Vertex Graph Theory
Graph Coloring Using Cuda I Team Members
Graph Coloring Github Topics Github
Star Coloring Wikipedia
Graph Coloring Or Proof By Crayon Math Programming
Decades Old Graph Problem Yields To Amateur Mathematician Quanta Magazine
Greedy Coloring Wikipedia
Color Graph Coloring Vertex Graph Theory Angle Symmetry Search Algorithm Media Transparent Background Png Clipart Pngguru
Graph Theory Edge Coloring Aresta Bipartite Graph Mathematics Angle Symmetry Png Pngegg
Graph Theory List Coloring Of Planar Graphs
Applications Of Graph Colouring Youtube
Ppt Graph Theory And Graph Coloring Lindsay Mullen Powerpoint Presentation Id 2065357
Star Coloring Wikipedia
Graph Colouring Computer Science Unplugged
Pdf 3 Consecutive Edge Coloring Of A Graph
Graph Theory
Edge Coloring From Wolfram Mathworld
Graph Coloring Applied Graph Theory Lecture Slides Docsity
Graph Coloring Or Proof By Crayon Math Programming
Solved 3 A In Graph Theory What Is Meant By Graph Colo Chegg Com
Color Background Png Download 1200 1065 Free Transparent Graph Coloring Png Download Cleanpng Kisspng
Math For Seven Year Olds Graph Coloring Chromatic Numbers And Eulerian Paths And Circuits Joel David Hamkins
Five Lessons I Ve Learned From B Coloring In Graph Theory In 2020 Color Puzzle Graphing Color
Graph Theory Graph Terminologies Planar Graph Graph Colouring
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcrwppgpcgckyoj47m4vma4cu5nmu1qzlkxjcukanfgmbz6 Z3z7 Usqp Cau
Introduction To Graph And Graph Coloring
Graph Coloring Vertex Graph Theory Time Complexity
Mathematics Planar Graphs And Graph Coloring Geeksforgeeks
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqh4zwiir4drrdbmsc1jmy2cojqihfxpepccz9hi76t5 Gbl36o Usqp Cau
Pdf Applications Of Graph Coloring
Graph Theory Coloring Tutorialspoint
Dominator Coloring Of Some Classes Of Graphs Semantic Scholar
Help Understanding A Solution Proof For A Problem In Graph Theory Coloring Mathematics Stack Exchange
Pdf General Pattern Of Total Coloring Of A Prism Graph Of Layers And A Grid Graph
Introduction To Graph Colouring Youtube
Graph Theory Coloring Tutorialspoint
Petersen Graph Theory Coloring Vertex Body Jewelry Matching Transparent Png
Vertex Coloring From Wolfram Mathworld
Point Triangle Mathematics Graph Vertex Graph Theory Graph Coloring Symmetry Graph Of A Function Free Png Pngfuel
Graph Coloring Or Proof By Crayon Math Programming
Computer Science Graph Coloring Graph Theory Vertex Mathematics Png Pngbarn
Chromatic Number Definition Examples Video Lesson Transcript Study Com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqxyvn3a Xq2k0hetpjbqzhopvn0jkgf5avaobt5ob6cmcy98cy Usqp Cau
The Four Color Theorem
Graph Theory Rld World
Coloring
Inventions Free Full Text Graph Theory A Comprehensive Survey About Graph Theory Applications In Computer Science And Social Networks Html
Graph Theory
A Sudoku Solver Using Graph Coloring Codeproject
Graph Coloring Chromatic Number With Solved Examples Graph Theory Classes In Hindi Youtube
Graph Edge Coloring Vizing S Theorem And Goldberg S Conjecture Wiley
Acyclic Coloring Graph Coloring Graph Theory Direc Number Theory Pfe2i Image Provided Epicentro Festival
Ams Feature Column From The Ams
Vertex Coloring Martin Thoma
Graph Coloring And Its Applications
Node Edge Coloring Of Graphs Mathoverflow
6 3 Graph Coloring Problem Backtracking Youtube
Chromatic Number From Wolfram Mathworld
Graph Theory Ch 5 Coloring Of Graphs 1 Chapter 5 Coloring Of Graphs Ppt Download
Graph Coloring And Its Applications
Graph Coloring Set 1 Introduction And Applications Geeksforgeeks
Graph Coloring In Graph Theory Chromatic Number Of Graphs Gate Vidyalay
Graph Theory Coloring Exploring Graph Theory
Rainbow Coloring Wikipedia
Edge Coloring Graph Coloring Graph Theory Petersen Graph Edge Png Nextpng
Graph Coloring Vertex Graph Theory Four Color Theorem Others Symmetry Color Bipartite Graph Png Pngwing
Graph Theory Brilliant Math Science Wiki
Graph Theory
Graph Theory Sample Exam I
Graph Theory
Graph Coloring Business Management Book Chapter Igi Global
Introduction To Graph Theory Lecture 13 Graph Coloring Edge Coloring Ppt Download
Graph Coloring In Graph Theory Chromatic Number Of Graphs Gate Vidyalay
Graph Coloring Theory Planar Four Color Theorem Mathematics Transparent Png
Vertex Coloring Graph Theory Lecture Slides Docsity
Total Coloring Wikipedia
Coloring
